안녕하세요! 제리입니다.
이번에도 DMQA 김성범 교수님의 ARIMA 모형 강의를 내용을 토대로 작성했습니다.
https://www.youtube.com/watch?v=ma_L2YRWMHI&list=PLpIPLT0Pf7IqSuMx237SHRdLd5ZA4AQwd&index=9
정상 프로세스 (Stationary Process) : 시간에 관계 없이 평균과 분산이 일정한 시계열 데이터
정상성 확인 (Autocorrelation Function 패턴)

Lag1 : 현 시점과 한 시점 미룬 데이터와의 차이
Lag2 : 현 시점과 두 시점 미룬 데이터와의 차이
PACF(Partial AutoCorrelation Function) :
특정한 패턴 없이 랜덤할 경우 stationary 하다고 할 수 있다 (정상)
Nonstationary Process (비정상 프로세스) : 평균 및 분산이 바뀌는 것을 확인 가능할 때

ACF가 줄어드는 경향이 보임 or 천천히 감소 증가 하면서 줄어드는 경향

1. AutoRegressive(AR) Model

- X변수가 Y의 Lag 변수라는 점
- 독립 가정이 위배 => LSE로 추정하지 못함
2. Moving Average(MA) Model

t시점의 에러와 과거의 에러들로 표현
연속적 에러 텀으로 y와의 관계를 모델링
3. ARMA Model
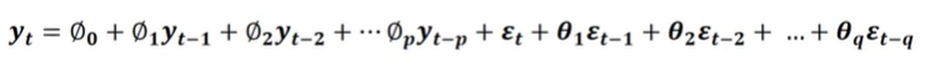
AR model과 MA 모델을 결합
4. ARIMA (AutoRegressive Integrated Moving Average)
위 세 개는 데이터가 stationary 해야함, nonstationary하면 안됨 => stationary하게 바꾸면 사용 가능 => 바꾸는 대표적인 방법으로는 differencing이라함
I에 따라서 differencing을 몇번했는지 보여줌
ARIMA 모델은 (p,d,q) 이렇게 있음. P는 AR의 변수 개수, Q는 MA의 변수 개수, d는 몇번 differencing 했는 지 표현
차분(Differencing) : 현 시점 데이터에서 d 시점 이전 데이터를 뺀 것
Nonstationary 데이터를 차분 과정을 거치면 stationary하게 주로 변화 됨.
한번 하는 것이 보통이고, 최대 2번 정도만 함
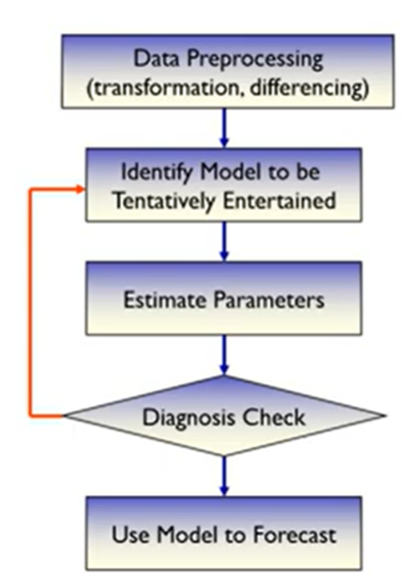
1. 데이터 전처리 : nonstationary한 데이터의 경우 stationary하게 바꿔줘야됨
2. 해볼 수 있는 모델을 찾기
3. 파라미터 추정
4. 모델 검정
5. 최종 모델로 예측
시범적 모델 찾는 방법 – Graphical method
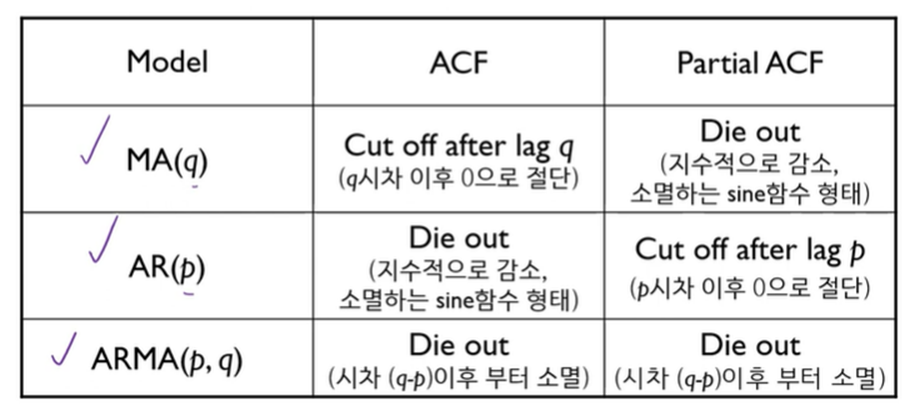
위 패턴일 경우 모델을 선정 – 주관적임
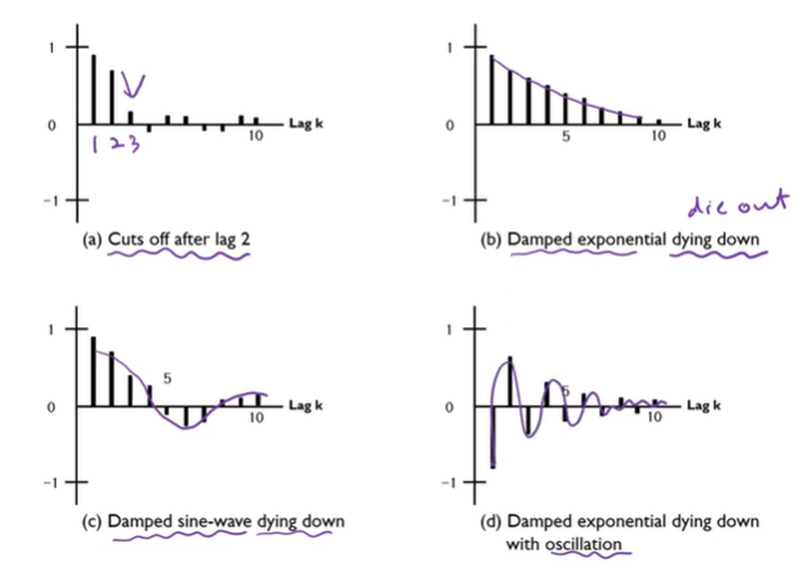
ACF와 PACF 그림을 보며 적합 모델을 임의 판단 후, 여러 개 비교해보며 AIC 작은 모델을 우선 선정
검증 – residual 값으로 ACF plot을 그래서 2~3개 정도 이상 기준 선 밖에 나가지 않는다면 좋은 거임 (3 시그마가 bound 임)
5. Seasonal ARIMA Model (SARIMA)
각 계절에 따른 독립적인 ARIMA 모델이 합쳐져 있는 모형
기존 ARIMA(p,d,q) 모형에 계절성 주기 차수 s가 추가 => ARIMA(p,d,q)(P,D,Q)s
월별 계절성인 경우 s = 12, 분기별 계절성인 경우 s = 4
7개의 파라미터를 정해줘야됨
'머신러닝' 카테고리의 다른 글
| 시계열 공부 (1) - 시계열회귀분석 (0) | 2023.06.27 |
|---|---|
| Statsmodels 이용한 시계열 분석에 대해 (0) | 2023.05.04 |
| pandas를 이용한 시계열 데이터 처리에 대해 (0) | 2023.05.03 |
| 클러스터링(군집화) 알고리즘에 대해 (1) | 2023.05.01 |
| Pandas에 대해 (Series, DataFrame) (0) | 2023.04.30 |



